Making 3D objects is a difficult thing. Some kind of guy has invented a way to quickly draw 3D objects on the screen. Our
teacher didn't tell us how to do that in 3D, just in 2D. But the main idea is the same. If you're able making Marching
Squares, the implementation of Marching Cubes shouldn't be a problem.
The idea behind Marching Squares is to devide de screen into little squares. Let's say you want to draw a certain curve,
which is given by the function
x^2 + y^2 = 2. This function is a circle with a radius of Sqrt(2). By the way, there's another implementation to draw circles
very quickly, which is based on Slope Search ( Searching ).
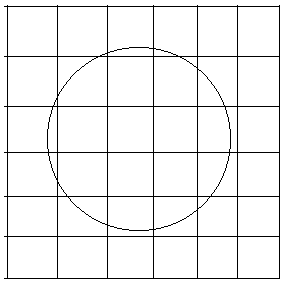
The circle will intersect withcertain squares like this:

The screen is devided into many squares. You have to go through every square to draw the curve. A square has 4 square-points. Go to each square-point and determine wheter the curve with function ( x^2+y^2=2 ) is above or below that point. If the curve is above that point you give that point an plus-sign. If the curve is below that point, you give that point an minus-sign. If the curve goes through that point, it's up to you wheter it's a plus or a minus. If you've done everything right you'll have given each square-point a sign plus or a minus.
Each square 4 sign. Each Square-point one sign. If a square only has minus signs you don't have to do anything, because you know the line is above the whole square. If the square only has plus signs you don't have to do anything too, because you know the curve goes below the square. So you only draw lines in a square if that square has minus-signs and plus-signs.
There are 4 different ways an minus and plus signs occur in a square:
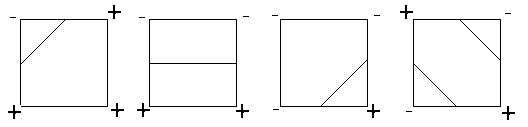
I have also drawn the lines in the squares. As told, you should draw a line if a plus and minus sign occur in a sqare. If they do. Then the line should be below the plus and above the minus as drawn in the this picture. Actually it's not very clear, but in the last picture it is clear you should drawn the 2 lines in the square on that way.
Okay that's all you need to know to implement the Marchin Cubes.
There is one problem: The result isn't as beautiful as you may think. Here are some pictures of the output:
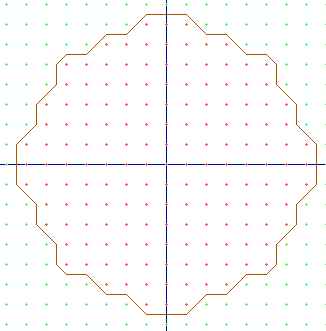
The red dots represent a minus sign. The green dots represent a plus. The blue lines are the x axis and the y axis. As yo see the result aren't as beautiful as you may wish. If you make the cubes smaller you will get a better circle, but the result is still very dissapointing. There are some ways to have a better output with bigger squares. One way I found out is by calculating the exact intersection-point of the curve with the sides of the squares. The calculation can be done by filling in the variables. That is no problem if you're function of the curve is an easy one, like y = x^4-3*x+2. But what if you're function is an ugly formula? Like x^3+y^3=2 ? Another way to approach the exact intersection-point is by using the Binary Search implementation ( Seaching ). The main idea is by calculating the sign on the middle of a side. If this sign is an plus, then you have reduced the side by an half. Repeat this process several times and you should find the intersection-point after several proceses. The approach explanation isn't very clear, but you should look to the explanation of Binary Search ( Searching ). Then you'll understand what I'm talking about.
After having calcuted the exact intersection-points and drawing the lines, you'll see that the output is pretty neat. And the squares doesn't have to be very small to have a nice circle:
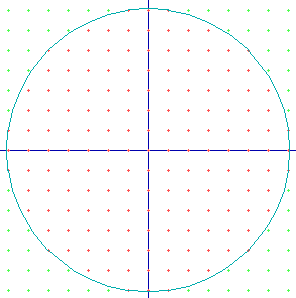
Well this circle really look like a circle doesn't it? So you know what to do next time. Better calculate the intersection-point and use bigger squares, so you don't have to go through that much squares.
I've got an implementation in Marching Squares. And I don't want to publish it. Because I find a lot of people to be
ungrateful. They download it without thanking or sending me a postcard. If you ask me nicely, then I may consider giving you
my implementation.